I was somewhat interested in this problem for some time.
After testing Dmitry’s smoother branch (smooth IS), I noticed that I can’t see the difference without adjusting max_error.
I was puzzled. Can I finally do something with it?
I initially was unable to grasp the original code in a way that would allow me to reimplement it. I have written different solutions from scratch several times :D, till I get the idea.
Sure, I think that I am still not able to write a good add fit function.
Now, I do have some understanding, and maybe I can add something useful.
If we define our problem as velocity jumps. Sure, it is in part due to the greedy algorithm.
But the other half of the problem is limited quantization and the quadratic function.
Like, for example, we cannot encode interval=1.5 or add=0.5.
So, there would be compression artifacts.
For the same reason, there is a theoretical limit to how good we can compress if we try to fit the raw data line.
I agree with the point that just decreasing max_error could improve the situation, and it will drop the compression ratio.
I can speculate on how much, depending on the MCU clock rate, microstepping & etc.
But, I suspect the main limitation of that way, it will limit the allowed fit for the oscillating flat lines.
Example:
// max error is mcu_freq * 0.000_025s
// Real data line is 2344, 2343, 2344, 2343... max error is 3750
// with 150MHz rp2350
queue_step oid=2 interval=2344 count=1172 add=0
queue_step oid=2 interval=2343 count=1172 add=0
queue_step oid=2 interval=2344 count=2231 add=0
// RP2040, max_error=300
queue_step oid=2 interval=188 count=188 add=0
queue_step oid=2 interval=187 count=188 add=0
queue_step oid=2 interval=188 count=188 add=0
queue_step oid=2 interval=187 count=188 add=0
There is a patch that does trim the outliners/underfitted tails.
That is it, if our fit does overshoot and the real data underneath has a different curvature/slope.
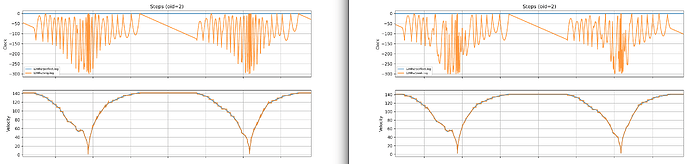
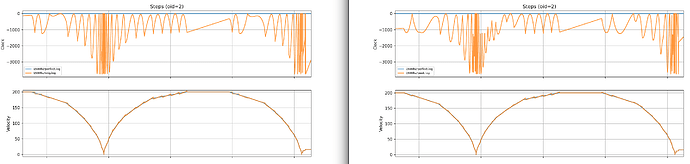
Below are the graphs.
Microstepping is set to 64. RP2040/RP2350 are just examples of different timer resoultions.
Compression ratio, I utilize the size of the serial output:
# Example 20min empty cube print
$ du -hs test_12Mhz*.serial
18M test_12Mhz.serial
20M test_12Mhz_trim.serial # +10%
$ du -hs perfect_150Mhz.serial test_150Mhz.serial test_150Mhz_trim.serial
792M perfect_150Mhz.serial # 1-2 steps per cmd
11M test_150Mhz.serial
17M test_150Mhz_trim.serial # +35%
# Sort of curve torture test, torus, gcode_arcs, gyroid infill 40min
$ du -hs Torus_12Mhz*
32M Torus_12Mhz.serial
36M Torus_12Mhz_trim.serial # +12%
$ du -hs Torus_150Mhz*
26M Torus_150Mhz.serial
40M Torus_150Mhz_trim.serial # +35%
Borked metrics from above script
test_12Mhz.log vs Reference:
Speed Comparison:
RMSE: 0.000000
MAE: 0.000000
Max Error: 0.000001
Correlation: 0.999919
Interval Comparison:
RMSE: 6.031088
MAE: 0.969365
Max Error: 299.000000
Correlation: 1.000000
Add Comparison:
RMSE: 8.210030
MAE: 0.806903
Max Error: 597.000000
Correlation: 1.000000
test_12Mhz_trim.log vs Reference:
Speed Comparison:
RMSE: 0.000000
MAE: 0.000000
Max Error: 0.000001
Correlation: 0.999921
Interval Comparison:
RMSE: 5.781919
MAE: 0.893169
Max Error: 299.000000
Correlation: 1.000000
Add Comparison:
RMSE: 8.080921
MAE: 0.791200
Max Error: 597.000000
Correlation: 1.000000
Speed Graphs, speed is constant / interval.
Green is where I zoom. I messed up file names. This is a 150MHz RP2350.
This is a 12MHz RP2040.
I messed up file names. This is a 150MHz RP2350.
Green is where I zoom, because with the trim, there is an overshoot
It seems to improve the fit. It also introduces its own artifacts, where the trimmed tail allows the next function to start overshooting sometimes. But overall, because of just more aggressive segmentation, it is smoother.
(They also could be dumped, but that, unfortunately, would increase the data rate further).
Thanks.
Now I also have my own implementation, but nothing special
Implementation.
More code, I hope it’s simpler. Sligtly slower. Also, less compression, closer fit.
The basic idea is heuristic analysis.
- Don’t bother with
add extremus, limit max count
- Work with derivatives - intervals, not real numbers.
- Split by flat lines, cache intervals, and min intervals (minp).
- Guess. Opportunistic split.
- Refit with Linear Least Squares.
- Trim. Well, It is where I got it.